Piezometrica e il ‘materasso’ savonese

Tornando al nostro “materasso”, abbiamo detto: “e non è finita” il peggio deve ancora venire ! Ed il fatto è avvenuto. Crolla viadotto della A6 tra Savona e Altare, Quando sembrava che i problemi legati all’allerta meteo fossero terminati, ecco presentarsi un disagio considerevole: chiuso il tratto di autostrada A6 Savona-Torino “La Verdemare” per un cedimento di un viadotto sul  troncone in direzione Torino che si incontra tra Savona e Altare prima della prima galleria.

Nel corso del fine settimana la Savona-Torino era stata letteralmente flagellata da movimenti franosi legati alle forti piogge, che avevano portato alla chiusura di alcuni punti. Un’ultima, ennesima frana, dovuta alla “piezometrica” sarebbe stata quella fatale, in grado di sferrare il “colpo di grazia” ai piloni del ponte.

Prima di addentrarci nella situazione dei liquidi reali mediante coefficienti correlativi ricavati, diamo alcune definizioni basilari.

In una massa d’acqua in movimento, definiamo come:

a – filetto liquido o linea di flusso: la traiettoria di una particella infinitesima di liquido; b – vena liquida o tubo di flusso: fascio di linee di flusso; c – corrente: l’insieme di più vene liquide o di tubi di flusso.

Possibili regimi di moto dell’acqua:

a – moto vario: avviene nei fiumi e nei torrenti in natura [regime torrentizio]; la sua caratteristica è data dalle vene liquide che variano di velocità e di pressione di sezione in sezione, e sono anche variabili nel tempo. b – moto permanente o stazionari:; si ha tale tipo di moto, allorché la velocità e la pressione delle vene liquide varia da sezione a sezione, ma non variano nel tempo [sono permanenti] c – moto uniforme: è il classico moto della dinamica; si ha allorché la velocità e la pressione delle vene liquide sono costanti da sezione a sezione e nel tempo.

Una corrente può scorrere in un condotto e può avere:

a – scorrimento turbolento: quando i liquidi, avanzando, si rimescolano tra di loro; b – scorrimento laminare: quando i filetti liquidi procedono parallelamente tra di loro e alla condotta, anche se a velocità relative variabili: velocità nulle in aderenza alle pareti del condotto, e massime in corrispondenza del “filone della corrente”

Comunque sia lo scorrimento dell’acqua nelle condotte, turbolento o laminare, si capisce che le velocità dei vari filetti non è costante nella sezione; perciò d’ora in poi, quando si parlerà di «velocità » dell’acqua s’intenderà sempre «velocità media dell’acqua» nella sezione considerata. In un condotto [tubo o canale, non importa] che abbia sezione variabile A1,, A2, A3, ect…la portata deve essere costante in tutte le sezioni. Ciò è sempre vero, salvo per il caso del moto vario o torrentizio, che però è escluso per il momento. Il concetto che abbiamo espresso è evidente, se si pensa all’incompressibilità dell’acqua e alle sue conseguenze.

Infatti in un condotto, privo di perdite, tanta acqua entra nella sezione A1 e tanta ne deve uscire da una qualsiasi altra sezione. L’acqua non può accumularsi lungo il percorso, essendo incompressibile, né rarefarsi, per la medesima ragione; quindi la quantità di liquido che entra in un condotto deve essere uguale alla quantità che ne esce.

Q1 = A1V1 = Q2 = A2V2 = Q3 = A3V3 =………Qn

Dall’Equazione di continuità, si evince che la portata del condotto è Q1 = A1V1 = 1 x1 = 1m3/s e che le velocità del liquido sono inversamente proporzionali all’area delle relative sezioni V2 = Q/ A2 ; in uno stesso condotto, maggiore è l’area di una sezione, minore è la velocità del liquido, viceversa minore è la sezione e maggiore la velocità. Dall’equazione di continuità discende un’altra importante conseguenza, infatti possiamo dire che in un condotto, la massa d’acqua che passa in ogni sezione è costante. Poiché sono costanti le portate Q lo sono anche i volumi [Q1 = vol/s] e moltiplicando il volume per il peso specifico, si ottiene pure costanti i pesi G1 = G2 ovvero G1 =m1g =G2 =m2g G = mg/g si ottiene m1 = m2 = m3 = cost.

Si consideri il movimento di un liquido perfetto nell’ipotesi di moto permanente: se il liquido si muove solo sotto l’azione della forza di gravità, come avviene in pratica per i canali e le condotte in pressione, tale moto è espresso dal «teorema o principio di Bernoulli» [] questo teorema non è altro che un’applicazione del «principio di conservazione dell’energia», adattato alla dinamica dei fluidi. Si consideri una condotta in pressione a sezione variabile, in cui scorra un liquido perfetto

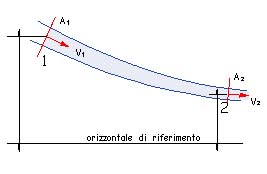Nell’unità di tempo la massa d’acqua che fluisce attraverso le sez, 1 e 2 di area A1 e A2 è costante Q1 = Q2 = costante

Dall’espressione dell’equazione di continuità; quindi anche il peso della massa d’acqua che scorre attraverso le due sezioni deve essere costante, cioè: G1 = G2 =m1g = m2g

Per il principio di Bernoulli, anche la somma delle energie che la massa unitaria d’acqua possiede, traslando attraverso le due sezioni 1 e 2, deve essere costante [applicazione del detto: nulla si crea e nulla si distrugge], quindi:

E = costante

L’energia posseduta dalla corrente d’acqua nella sez. 1 è espressa nella sommatoria delle seguenti tre forme energetiche:

● Energia potenziale o di posizione

Tale energia equivale al lavoro che potrebbe compiere il peso G1 d’acqua, qualora cadesse dall’altezza h1 sul piano di riferimento [nell’unità di tempo]. Cioè: Epot = G1h1 = m1gh1

● Energia cinetica

Tale energia è prodotta dalla V1 della corrente che transita per la sezione 1 [nell’unità di tempo]; essa vale:

Ecin = 1/2 m1V12

● Energia di pressione o piezometrica

È data dal lavoro che produce la pressione P1 spostando la sez. A1 in uno spazio s1 nell’unità di tempo. Perciò: l’espressione della pressione è: P1 =A1h1 γa = A1p1

inoltre, nell’unità di tempo, lo spazio percorso è uguale alla velocità cioè: s1 = V1 quindi l’energia piezometrica vale: Epi = P1V1 = p1A1V1 = p1Q1 = p1 [m1g/ γa]

La portata Q può essere espressa nel seguente modo: m1g = G1 = Q1 γa cioè Q1 = m1g/ γa che sostituito nella precedente espressione dell’energia piezometrica:

Epi = p1 [m1g/ γa]

La Ʃ delle espressioni delle tre energie relative alla sezione 1, porge: E1 = m1gh1 + 1/2 m1V12 + p1 [m1g/ γa]

Analogamente l’espressione della sommatoria delle energie relative alla sezione 2 sarà: E2 = m2gh2 + 1/2 m2V22 + p2 [m2g/ γa]

Il principio di conservazione dell’energia o di Bernoulli afferma che: E1 = E2 e il principio della continuità afferma che: m1 = m2 = m, quindi le due espressioni divengono l’unica equazione: m1gh1 + 1/2 m1V12 + p1 [m1g/ γa] = m2gh2 + 1/2 m2V22 + p2 [m2g/ γa] = costante

dividendo l’equazione per il peso costante mg si ha infine: h1 + V12/2g + p1 / γa = h2 + V22/2g + p2 / γa = cost.

tale espressione è l’importantissima equazione del Bernoulli, della quale è essenziale esaminarne il significato pratico.

La linea piezometrica è il luogo dei punti in cui la pressione relativa in un fluido è nulla. Questa linea rappresenta la quota che raggiungerebbe un fluido (in una condotta) se fosse lasciato libero. Tale linea, rappresenta il pelo libero che il fluido avrebbe se non fosse sottoposto ad alcun vincolo. Solitamente si parla di linea piezometrica nel caso in cui il fluido sia in movimento: in caso contrario si parla di piano dei carichi idrostatici.

Nel caso in cui il fluido non si trovi sottoposto a pressione, essa coincide con la superficie di separazione tra il fluido stesso e l’atmosfera. Nel caso in cui fosse sottoposto ad una pressione all’interno di una condotta, la linea piezometrica si troverà al di sopra del volume di liquido; viceversa avverrà se il liquido è in una condotta in depressione.

Se il liquido (un fluido reale) è in movimento la linea piezometrica avrà un’inclinazione negativa. Questo avviene perché un liquido in movimento utilizza parte della propria energia per contrastare le dispersioni di energia dovute alla propria viscosità e turbolenza e agli attriti con la superficie della condotta. La sua inclinazione, che prende il nome di cadente piezometrica, rappresenta la perdita di carico idrodinamico per unità di lunghezza e per unità di peso di fluido, e dipende dalla viscosità del fluido in movimento e dalla scabrezza della condotta (si tratta dunque di una perdita distribuita), cioè da quanto essa è ruvida e quindi si oppone al movimento della massa di liquido. La linea piezometrica può subire brusche cadute provocate dalla presenza di bruschi allargamenti, bruschi restringimenti o curve nella condotta. Si parla in questo caso di perdite di carico. La linea piezometrica dà un’indicazione relativamente all’andamento del carico totale lungo il percorso del moto. Specialmente quando si parla di correnti in pressione che di per sé sono caratterizzate da un termine cinetico costante essa si traccia proprio parallelamente alla linea dei carichi totali. Inizialmente si era accennato all’attrito interno ed esterno dell’acqua in movimento, ma poi per semplicità di ragionamento si era considerato il liquido perfetto, cioè privo di attriti. Ora, invece esaminiamo i liquidi con attrito.

L’attrito interno [tra le particelle d’acqua] e molto di più, l’attrito esterno [fra particelle d’acqua e condotta] provocano una perdita di energia lungo la condotta che si usa indicare come «perdita di carico continua Y». Essa è dovuta ad una trasformazione di energia meccanica in energia termica, per effetto, appunto, degli attriti. In altre parole alle tre energie [potenziale, cinetica e piezometrica] possedute dalla massa d’acqua nella sezione 1 di condotta, bisogna aggiungere un’energia termica. Tale energia andrà crescendo, per effetto degli attriti, e passando dalla sez. 1 alla sez. 2, la massa d’acqua sarà più calda [possederà più energia termica], proporzionalmente alla lunghezza del percorso L. Per la verità la dizione «perdita di carico continua Y» non è esatta, sarebbe meglio dire «trasformazione di energia piezometrica in energia termica » [infatti le altre due energie non possono mutare, perché le altezze geometriche h1 e h2 sono fisse, ed anche la velocità rimane costante, legata all’equazione di continuità]. Tuttavia poiché il piccolo aumento di temperatura che l’acqua subisce lungo il percorso non è sfruttabile utilmente, è proprio come se andasse perduta una certa quantità di energia. L’equazione di Bernoulli per i liquidi reali è:

h1 + V12/2g + p1 / γa = h2 + V22/2g + p2 / γa + Y

Per liquidi reali nel caso di tubo a sezione costante è rappresentato (BER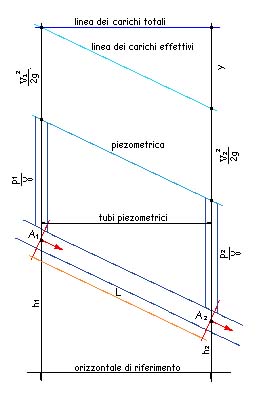NOULLI 2)

l’aggiunta di due tubi piezometrici in corrispondenza delle sezioni 1 e 2. Come si può constatare, l’acqua risale nei due tubi verticali per effetto della pressione unitaria posseduta nelle due sezioni, di altezza pari a p1 / γa e+ p2 / γa; le due altezze cinetiche V12/2g e V22/2g [perché A1 = A2] non raggiungono più la medesima quota, ma compare, invece l’altezza Y [perdita di carico]

che va aggiunta alle altre altezze relative alla sezione 2.

In conclusione si ha una linea dei carichi totali [orizzontale]. Che rappresenta la costante delle energie nelle varie sezioni di condotta; una linea dei carichi effettiva o disponibili, che rappresenta lo stato energetico sfruttabile; la linea piezometrica che, al solito, rappresenta la quota a cui l’acqua può risalire per effetto della sola sua pressione unitaria.

●
Per tubi a sezione costante, le linee dei carichi effettivi e dei carichi piezometrici, sono parallele [ma in genere non sono parallele alla condotta]

● Il valore della perdita di carico Y è dato dalla differenza delle quote piezometriche [essendo le due quote cinetiche uguali]

● Per le condotte non in pressione, ma a pelo libero come i canali, la linea dei carichi piezometrici coincide con il pelo libero dell’acqua; infatti è impensabile che l’acqua di un canale risalga spontaneamente, di una certa altezza, un tubo verticale immerso in essa.

● Il valore della perdita di carico Y, in un canale è dato dalla differenza delle quote altimetriche h1 e h2 solamente [ammessa sempre l’ipotesi delle sezioni costanti, e quindi V1 = V2]: h1 – h2 = Y. Nei terreni o masse di natura differente, con trovanti [], ogni squilibrio tra coesione, attrito e gravità genera perturbazioni statiche che si manifestano in tre modi diversi.

● Scoscendimenti. Quando per effetto di calore o d’intervento di variazioni atmosferiche, l’acqua contenuta nelle masse terrose evapora, le terre subiscono un ritiro perdendo la loro coesione e finiscono per scoscendere. Ogni scoscendimento può anche portare con sé anche scivolamento di trovanti; in genere gli scoscendimenti si manifestano in superficie. [Slavine]

● Smottamenti. Sono movimenti superficiali che si verificano quando le terre sono sature d’acqua ed hanno oltrepassato il normale limite di liquidità [LL], per cui, tendono a diventare fluide. L’angolo di natural declivio φ tende a 0 in rapporto alla quantità d’acqua imbevuta.

● Frane. Nella pluralità dei casi si manifestano per la mancata registrazione delle acque, che, penetrando nel terreno favorevole, fanno slittare la massa sovrastante [permeabile] su di un’altra inferiore [impermeabile] divisa da un piano di natura differente detto piano di scorrimento. Poiché per frane s’intende il distacco lento o repentino di una massa dall’originale, sarebbe opportuno definire la frana come: «movimento rapido o lento di masse che si staccano dall’originale, verso valle». Le frane possono essere superficiali o profonde; le prime sono quelle azionate da acque scorrenti in superficie che rompono l’equilibrio, le seconde quando le acque, scorrendo in profondità, su piani impermeabili, generano movimenti di masse, che a volte possono raggiungere dimensioni e volumi inimmaginabili. [Valanghe]. Nelle costruzioni stradali lo smaltimento delle acque, il prosciugamento della piattaforma riveste una importanza fondamentale anche se per tanto tempo ne fu sottovalutata l’importanza. L’acqua rappresenta la “tubercolosi” della strada. Le acque capillari tendono a risalire specialmente nel periodo delle piogge e delle morbide [Stato di regime intermedio dei corsi d’acqua, che si verifica allorché le acque si gonfiano per effetto di piogge o di disgelo, senza raggiungere i livelli di piena] dei corsi d’acqua.

In ragione della quantità d’acqua contenuta in un terreno, varia la capacità portante del terreno stesso. Tale capacità aumenta con il diminuire dell’acqua; non solo coll’aumentare del tenore acqua nei terreni argillosi il volume del terreno cresce fino a disintegrare la fondazione di una qualsivoglia struttura. Dell’acqua piovana, cadendo sulla superficie terrestre, una porzione [20-25%] evapora; un’altra corre sul terreno stesso; un’altra viene assorbita dalle piante. La percentuale d’acqua assorbita, saturando il terreno ed incontrando due strati più resistenti viene a formare, tra essi, uno strato d’acqua detto: falda acquifera o fratica. La falda freatica è il primo strato che s’incontra a partire dal piano di campagna.

Si chiama «superficie basale piezometrica» il piano superficiale dell’acqua interna del terreno rispetto al piano di campagna. Tale livello non è mai costante per effetto delle fluttuazioni lente e disuguali della falda, la quale è soggetta a una serie di influenze diverse quali forze di precipitazioni atmosferiche specie se attraversano rocce porose che si lasciano invadere velocemente [vedi th. Di Bernoulli]. La linea di una falda non è mai orizzontale ma una curva ad andamento sinusoidale, leggero o sensibile che tende ad adattarsi all’andamento ed alle ondulazioni dello strato impermeabile; si alza sotto le colline, si appiattisce in corrispondenza delle valli. []. L’andamento di ogni linea piezometrica tende ad inclinarsi verso la sorgente di scolo o raccolta d’acqua [fiumi, canali, drenaggi] e l’andamento della linea è concava, mentre diventa convessa, quando il tratto è solcato da due corsi d’acqua come avviene fra due fossi, fra due drenaggi, …ect.

La quantità d’acqua assorbita è quella che scorre in superficie ed è in funzione al tipo di terreno; maggiore sarà l’acqua assorbita minore sarà il deflusso. L’attrito che incontra l’acqua nello scorrimento interno del terreno varia con la natura di esso, gli strati di separazione, le condizioni atmosferiche; resta invariato il deflusso esterno. Nel sottosuolo, l’acqua cammina attraverso le ferritoie naturali, le separazioni dei differenti strati, i vani [detti comunemente pori o vuoti] che si distinguono in capillari o non capillare a seconda la loro dimensione. I primi sono quelli di sezione tale da permettere l’ascensione dell’acqua; la somma dei pori capillari viene definita volume dei pori.

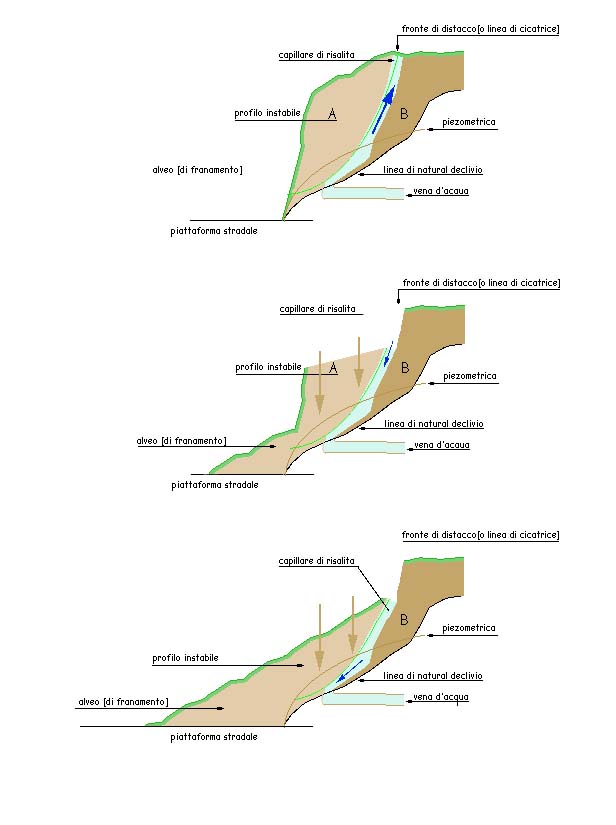In conclusione quando i capillari quelli che permettono l’ascensione dell’acqua vanno prima in stand by poi incominciano a regredire [colonna d’acqua] ecco che si presenta, puntuale, il problema “frana”. Il peso del terreno a valle della colonna d’acqua fa si che le molecole cui è composto si “asciughino” ovvero si ricompattano tra loro ed esercitano una o più forze di scorrimento che fanno precipitare il tutto a valle.

Alesben B.